 |
biomcmc-lib
0.1
low level library for phylogenetic analysis
|
 |
biomcmc-lib
0.1
low level library for phylogenetic analysis
|
Random number generation, with algorithms from the Gnu Scientific Library (GSL) and motivation from the Scalable Parallel Pseudo Random Number Generators Library (SPRNG). More...
#include "random_number_gen.h"
Go to the source code of this file.
Data Structures | |
| struct | biomcmc_rng_struct |
| Random number structure (combined Tausworthe algorithm) More... | |
Typedefs | |
| typedef struct biomcmc_rng_struct * | biomcmc_rng |
Functions | |
| void | biomcmc_random_number_init (unsigned long long int seed) |
| High-level setup of a simple random number generator and initialization with a seed (not to be mixed with other low-level functions that update the seed or allocate memory). More... | |
| void | biomcmc_random_number_finalize (void) |
| High-level finalization (memory release etc.) of the random number environment. | |
| biomcmc_rng | new_biomcmc_rng (unsigned long long int seed, int stream_number) |
| Allocate memory for new (Tausworthe + MT19937) generator from a pool of streams. | |
| void | del_biomcmc_rng (biomcmc_rng r) |
| Release memory occupied by biomcmc_rng:: | |
| unsigned long long int | biomcmc_rng_get_initial_seed (void) |
| Create initial seed based on time, combining time in microseconds and seconds (user-controled seed is not uint64_t) | |
| biomcmc_rng | new_biomcmc_rng_from_seed (unsigned long long int seed, int stream_number) |
| Generate a vector of seeds (based on initial one), create and initialize stream with an element of this vector. | |
| double | biomcmc_rng_snorm32 (void) |
| Returns a random number from a Standard Normal distribution N(0,1) - prob_distribution.h has general case. | |
| double | biomcmc_rng_snorm (void) |
| Returns a random number from a Standard Normal distribution with maximum (52 bits) integer precision. | |
| double | biomcmc_rng_unif (void) |
Returns a random number between 0 and 1 (including 1) with precision 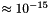 (52 bits). (52 bits). | |
| double | biomcmc_rng_unif_pos (void) |
| Returns a positive random number between 0 and 1 (excluding 0 and including 1) (52 bits). | |
| uint64_t | biomcmc_rng_unif_int64 (uint64_t n) |
Returns a long integer (64 bits) random number between 0 and n (excluding n), with 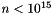 . . | |
| double | biomcmc_rng_unif32 (void) |
Returns a random number between 0 and 1 (including 1) with precision 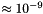 (32 int bits). (32 int bits). | |
| double | biomcmc_rng_unif_pos32 (void) |
| Returns a positive random number between 0 and 1 (including 1) (32 int bits). | |
| uint32_t | biomcmc_rng_unif_int (uint32_t n) |
Returns an integer (32 bits) random number between 0 and n (excluding n), provided 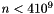 approx. approx. | |
| uint64_t | biomcmc_rng_get (void) |
| new value with 64 random bits | |
| double | biomcmc_rng_get_52 (void) |
| new value with 52 random bits as a double precision float | |
| uint32_t | biomcmc_rng_get_32 (void) |
| new value with 32 random bits | |
| void | biomcmc_get_time (int *time) |
| get current time with maximum precision and soter in vector time[2] | |
| double | biomcmc_elapsed_time (int *now, int *past) |
| returns the floating-point time in seconds elapsed between past[2] and now[2] | |
Variables | |
| biomcmc_rng | biomcmc_random_number |
| pointer to pseudo-random number generator (should point to real stream, even when there are several) | |
Random number generation, with algorithms from the Gnu Scientific Library (GSL) and motivation from the Scalable Parallel Pseudo Random Number Generators Library (SPRNG).
There are two ways of setting up the pseudo-random number generation: a high-level approach where we simply call one function before start using the generator and another after we finished using it, and a lower-level approach where we must allocate, seed and free the streams by hand. Both approaches are completely incompatible, and there is no check to avoid this mistake so the programmer should use the first, high-level approach unless he understand well the algorithms. The high-level approach is useful when one stream is enough (for instance, a serial program). In this case we use a (modified) maximally-equidistributed combined Linear Feedback Shift Register (LFSR, or Tausworthe) pseudo-random number generator (PRNG) whose seed is based on time of day.
The low level approach is useful if one needs several uncorrelated streams - for example a parallel program where each node must have its own stream of pseudo-random numbers and a common stream shared by all nodes. For this we implemented a modified random tree method where a lagged-Fibonacci generator (two-tap Generalised Feedback Shift Register - GFSR4) PRNG is used to generate the seeds for the (modified) Tausworthe streams. The seed for this GFSR4 generator is given by the time of day and should be set only once by the program, given its low randomness. The GFSR4 uses a vector of size 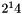 which is initialized by an (quick-and-dirty) xorshift randomization of the seed, which makes it sensitive to the choice of this seed. I included a gamerand fast randomization over each element of the vector, modified for 64 bits (the algorithm is too simple to require a license and I've seen public domain versions of it; the original disclaimer is GPL-like). A more robust alternative not implemented here would be to use a better PRNG to feed the initial vector of the GFSR4 generator. As noticed by CJK Tan and JAR Blais (HPCN 2000, LNCS 1823, 127-135) another random tree method could be constructed with parallel GFSR4 streams where the initial states are created by an PRNG - equivalent to our seed generator, but providing not only the seed but all
which is initialized by an (quick-and-dirty) xorshift randomization of the seed, which makes it sensitive to the choice of this seed. I included a gamerand fast randomization over each element of the vector, modified for 64 bits (the algorithm is too simple to require a license and I've seen public domain versions of it; the original disclaimer is GPL-like). A more robust alternative not implemented here would be to use a better PRNG to feed the initial vector of the GFSR4 generator. As noticed by CJK Tan and JAR Blais (HPCN 2000, LNCS 1823, 127-135) another random tree method could be constructed with parallel GFSR4 streams where the initial states are created by an PRNG - equivalent to our seed generator, but providing not only the seed but all 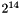 elements to each stream. To ensure independence of streams - since different seeds are just different points of the same stream - we implemented all 150 parameter sets provided by L'ecuyer (Maths Comput 1999, pp.261)for the Tausworthe generators. So we have at least 150 independent streams, with periods between
elements to each stream. To ensure independence of streams - since different seeds are just different points of the same stream - we implemented all 150 parameter sets provided by L'ecuyer (Maths Comput 1999, pp.261)for the Tausworthe generators. So we have at least 150 independent streams, with periods between 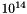 and
and 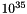 - if I understood correctly the interpretation of the number of non-zero solutions of the polynomials
- if I understood correctly the interpretation of the number of non-zero solutions of the polynomials 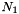 .
.
Our modification to the original Tausworthe (LFSR) algorithms is to combine it with the generalized Marsaglias's xorshift PRNG called xorgens, developed by Richard Brent and available under a GPL license. So the LFSR has one extra component from this independent xorshift (combined through a XOR). The seed for the xorshift is the same as for the Tausworthe.
All streams are of 64 bits (dependent on a "long long int" having 64 bits) but 32 bits or even 16 bits are available through wrapper functions. If your system does not provide 64 bit integers use the unwrapped versions instead. When working with more than one stream at the same time - by the same node, using the example of a parallel program - we must update by hand the variable pointed to by the global variable ::random_number to indicate which stream should be used.
Some original comments from the GSL can be found on "doc/random_number_generation.txt"
| void biomcmc_random_number_init | ( | unsigned long long int | seed | ) |
High-level setup of a simple random number generator and initialization with a seed (not to be mixed with other low-level functions that update the seed or allocate memory).
The seed may be provided by calling function (mostly for debug) if not zero otherwise it is based on present time of day, and uses the Tausworthe pseudo-random number generator. The Tausworthe generator we use has a period of (at least?) 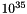 . This function allocates memory to global variable ::random_number directly
. This function allocates memory to global variable ::random_number directly
 1.8.13
1.8.13